Handcraft Ray Tracing
本文将介绍如何手搓光线追踪。先上效果图:


代码仓库:handcraft-MVS。
实现了:
- 漫反射
- 基于菲涅尔定律的折射与反射
- 允许多光源
- 球体相交检测
TODO:
- 其他几何体的相交检测
- 另起一篇实现光栅化
简介
通过程序模拟光线从光源发出后到达相机光心的路径,来渲染出接近现实光照变化的图像。
漫反射的实现
本节考虑的物体表面都只会发生漫反射。漫反射是指,由于物体表面的粗糙,一束光线击中表面后,会向各个方向反射,反射光线与入射光线角度越大,反射光线的强度越弱。
最朴素的思考则是从光源出发,思考光线的传播,所谓 正向。考虑只有单次漫反射这一最简单的情况,当光源发出的光线第一次打到物体时,如前文所述,会向各个方向反射,而这么多法反射的光线中,只有穿过成像平面的光线是对渲染有意义的,其余的反射光线我们则不关心。
因此,利用光路的可逆性,我们反过来思考,所谓 反向:
- 从相机光心出发射出一条光线,判断是否会打到物体表面的一个点上
- 若能打到,再从这个点上发出一条光线,判断是否会打到光源上
- 若能打到,则可以计算出该视角下该点的像素值
因此,反向 的思路更适合代码实现。伪代码如下:
// retval: surface_color
vec3 trace(const vec3& ray_ori,
const vec3& ray_dir,
const vector<ObjSharedPtr>& objs,
int depth)
{
obj_ptr = nullptr;
getClosestHitPt(ray_ori, ray_dir, objs, &obj_ptr, &t);
if (obj_ptr == nullptr ) return vec(0.1, 0.1, 0.1);
pt_hit = ray_ori + ray_dir * t;
norm_hit = obj_ptr->calNormHit(pt_hit);
for (light: lights) {
shadow_ray_dir = norm(light->center_ - pt_hit);
is_shadow = checkIntersect(pt_hit+norm_hit*eps, shadow_ray,dir);
if (is_shadow) continue;
ratio = max(0.0, norm_hit.transpose() * shadow_ray_dir);
surface_color += ratio * light->emission_color_;
}
surface_color += obj_ptr->emission_color_;
return surface_color;
}
折射与反射的实现
菲涅尔方程组 与 递归实现 为两个核心。
菲涅尔方程组
菲涅尔方程组 描述了光线在两种介质分界处反射和折射的现象。给定入射角 $\theta_i$,两种介质的折射指数 $n_1$ 和 $n_2$,能够利用该方程组计算出反射角 $\theta_r$、折射角 $\theta_t$、反射率(反射能量占比) $K_r = R_{eff}$ 、折射率 $K_t = i - K_r$。
\[\theta_r = \theta_i\] \[\sin \theta_t = \min ( 1, \frac{n_1}{n_2} \sin \theta_i ) \Leftarrow n_1 \sin \theta_i = n_2 \sin \theta_t\] \[r_s = \left | \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t} \right |\] \[r_p = \left | \frac{n_2 \cos \theta_i - n_1 \cos \theta_t}{n_2 \cos \theta_i + n_1 \cos \theta_t} \right |\] \[R_{eff} = \frac{R_s + R_p}{2} = \frac{r_s^2 + r_p^2}{2}\] \[K_r = \min (1, R_{eff})\] \[K_t = 1 - K_r\]值得注意的是,当从光密介质射向光疏介质,即 $n_1 > n_2$ 时,可能存在 $\frac{n_1}{n_2} \sin \theta_i > 1 $ 的情况,此时 $\sin \theta_t$ 应被限制为 1,否则无意义。此时 $\cos \theta_t = 0 \Rightarrow R_{eff} = 1$,即全反射。
一般来说,真空的折射指数为 1,水晶的折射指数为 1.54。如果我们把一个介质的折射指数填得很大,那么就可以表现全反射,仿佛镜面反射一样。
以上考虑的都是光线不会被介质吸收,如果是金属,则粗略的讲金属的折射指数是复数,光线照射到金属上后有一部分的能量会被吸收。
递归实现
对于折射和反射,我们同样可以从 正向 和 反向 来思考。同样的,反向 的思路会更适合代码实现,且是以递归的形式。
这次我们先从反向的角度来思考,再正向的角度分析它的合理性和局限性。首先从相机光心发出某个朝向的一条光线,光线打到一个光滑物体,会分成反射和折射两部分,角度和分量则由菲涅尔方程给出。接下来我们对反射和折射的部分做同样的相交判断和计算,如果遇到光源或达到最大递归深度,则停止,然后回溯计算融合后的光线。
\[L_i \rightarrow K_r L_r + K_t L_t\]如果正向思考,哪些光线会进入相机,根据光路可逆,就是上文提到的反射和折射方向,从这两个方向入射的光线,都会有一部分的光进入相机:
- 对于从反射方向入射的光,其反射分量会进入相机
- 对于从折射方向入射的光,其折射分量会进入相机
- 而 $K_{rt}L_r$ 和 $K_{tr}L_t$ 分量则会射向其他方向,继续折射或反射,最终可能其部分分量会进入相机,仿佛是一个特定方向的光源,但这部分其实是非忽略了,这就是该算法的近似部分。这会导致水晶球的影子是全黑的,而不是光线穿过一部分。
对于从反射方向入射的光,其入射角等于原来的反射角,由 反射角等于入射角 可得。所以
\[\theta_{ri} = \theta_i \rightarrow \theta_{rt} = \theta_t \rightarrow \boxed{K_{rr} = K_r}\]对于从折射方向入射的光,其入射角为原来的折射角,其折射角为原来的入射角,因为
\[\left. \begin{align} n_1 \sin \theta_{tt} &= n_2 \sin \theta_{ti} \\ \theta_{ti} &= \theta_t \end{align} \right \} \Rightarrow \theta_{tt} = \theta_i\]以防忘记,再次给出 $r_s$ 和 $r_p$ 的表达式,我们只需对变量进行替换即可 $\theta_i \leftarrow \theta_{ti} = \theta_t$,$\theta_t \leftarrow \theta_{tt} = \theta_i$
\[r_s = \left | \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t} \right | , r_p = \left | \frac{n_2 \cos \theta_i - n_1 \cos \theta_t}{n_2 \cos \theta_i + n_1 \cos \theta_t} \right |\]可以发现 $r_{ts} = r_p$,$r_{tp} = r_s$,所以新的反射率不变,新的折射率 $K_{tt}$ 也不变,即
\[\left. \begin{align} R_{t_{eff}} &= R_{eff} \\ K_r &= R_{eff} \\ K_t &= 1 - K_r \end{align} \right \} \Rightarrow \boxed{K_{tt} = K_{t}}\]所以
\[\boxed{L_i \leftarrow K_{r} L_{r} + K_{t} L_{t}}\]仿佛光是从相机出发,然后反射和折射,虽然实际情况是外部的光线经过折射和反射进入相机。
球体的相交检测
着色器(shader)的实现
为每个像素的 RGB 通道分配一个值,这便是着色器所作的事。
动机来源:Graphics API is irrelevant - Tsoding
参考
- 3D Computer Graphics Primer: Ray-Tracing as an Example
- An Improved Illumination Model for Shaded Display. Turner Whitted, 1980
- 详解NeRF中的NDC ray space
附录
反射变换的矩阵表示
\[\mathbf{H_w = I - 2ww^T}, \mathbf{H_n = I - 2nn^T}\] \[\mathbf{|s|e = H_w s = H_n (-s)}\]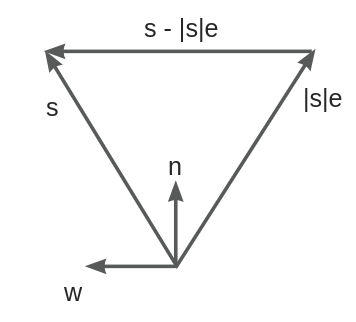
NDC 坐标系
简单来说,就是把视锥内的空间,变换到正方体空间中。