longer95479@home:~$

Archive

About

Categories

Tags

RSS

Singular Value Decomposition(SVD)

Eigen Vector Decomposing

特征值与特征向量的定义和关系可由下面等式给出

\[Ax = x\lambda\]

扩展成 n 个特征向量和特征值，有

\[A \begin{pmatrix} x_1 & x_2 & \cdots & x_n \end{pmatrix} = \begin{pmatrix} x_1 & x_2 & \cdots & x_n \end{pmatrix} \begin{pmatrix} \lambda_1 \\ & \lambda_2 \\ && \ddots \\ &&& \lambda_n \end{pmatrix}\]

简写为

\[AP= P\Lambda\] \[A= P \Lambda P^{-1}\]

这意味着什么呢？可以从这几个角度理解：

  • $A$ 与 $\Lambda$ 相似。两个矩阵相似，代表着同一个线性变换，在不同基下的表示。 $P$ 表示的是坐标系变换，$\Lambda$ 表示的是线性变换：
\[^{B_1}v \mapsto \ ^{B_1}w = A \ ^{B_1}v\] \[^{B_2}v \mapsto \ ^{B_2}w = \Lambda\ ^{B_2}v\] \[\begin{align} ^{B_1}w &= P \ ^{B_2}w \\ &= P \Lambda \ ^{B_2}v \\ &= P \Lambda P^{-1} \ ^{B_1}v \end{align}\]
  • A 这个线性变换被分解为三步（假设 P 正交）：先旋转，后拉伸，再旋转回去

PS:已知 $v \mapsto w,\ v,w \in \mathbb{R}^n$，需要 n 个这样的映射才能唯一确定一个线性映射或矩阵

\[\begin{pmatrix} v^T & 0_{1\times n} & \cdots & 0_{1\times n}\\ 0_{1\times n} & v^T & \cdots & 0_{1\times n}\\ \cdots && \ddots\\ 0_{1\times n} & 0_{1\times n} & \cdots & v^T\\ \end{pmatrix}_{n\times n^2} \begin{pmatrix} a_{11} \\ a_{12} \\ \dots \\ a_{1n}\\ \cdots\\ a_{nn} \end{pmatrix}_{n \times n} = w\]

SVD

full matrices:

\[A_{mn} = U_{mm}\Sigma_{mn}(V_{nn})^T\]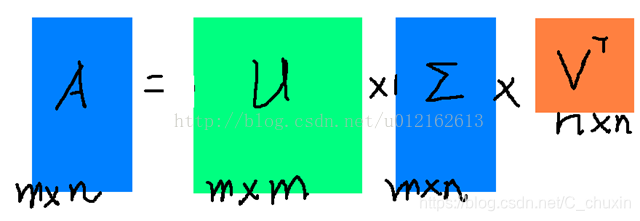

full_matrices

not full matrices: retain max r eigen values and vectors

\[A_{mn} \approx U_{mr}\Sigma_{rr}(V_{nr})^T, r \leq min(m,n)\]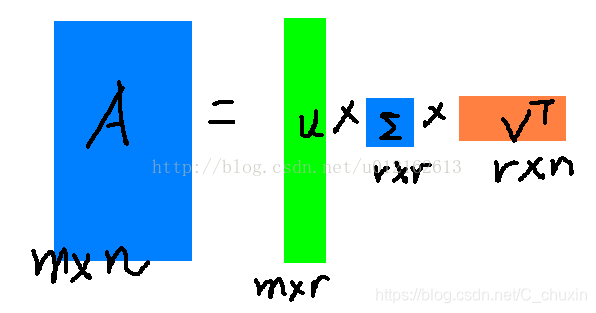

not_full_matrices

应用

图片压缩或降维

import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np

I = mpimg.imread("E:\\Data\\Pictures\\Screenshots\\屏幕截图(1).png");

u, s, vh = np.linalg.svd(I[:,:,0],full_matrices=False)
smat = np.diag(s)
print(smat.shape)

k = 5
I_compress = np.dot(u[:,0:k],np.dot(smat[0:k,0:k],vh[0:k,:]))

plt.subplot(2,1,1)
plt.imshow(I[:,:,0])
plt.subplot(2,1,2)
plt.imshow(I_compress)
plt.show()

求超定齐次方程 $Ax = 0$ 的最小二乘解

\[A_{mn}x = 0\] \[m>n,rank(A) = n\]

这个方程没有非零解（因为列向量空间维数是 m，但不相关的列向量只有 n 个，无法线性组合得到零向量），因此求最小二乘解，也就是让 $\lvert Ax \rvert ^2 = x^TA^TAx$ 最小的 x。

\[\begin{align} x^* = \underset{x}{\mathrm{arg\ min}}\ x^TA^TAx \\ s.t.\ x^Tx = 1 \end{align}\]
  • 如果 $x$ 是 $A^TA$ 的特征向量，在此前提下选择最小特征值对应的 x，则 $x^TA^TAx = \lambda$ 是最小的
\[x^TA^TAx = x^T \lambda x = \lambda x^Tx = \lambda\]
  • $x$ 不是 $A^TA$ 的特征向量
\[A = U \Sigma V^T \\\] \[A^TA = V\Sigma^T U^T U\Sigma V^T = V\Sigma^T\Sigma V^T \\\] \[x 用 V 的正交列向量表示：x = Va,\ a^Ta = 1\\\] \[\begin{align} x^TA^TAx &= x^T V\Sigma^T\Sigma V^T x \\ &= a^T \Sigma^T \Sigma a \\ & = \sum_{i=1}^{n} a_i^2 \lambda_i \geq \lambda_{min} \end{align}\] \[\lambda_{min} = \sum_{i=1}^n a_i^2 \lambda_{min} \leq \sum_{i=1}^{n} a_i^2 \lambda_i \leq \sum_{i=1}^n a_i^2 \lambda_{max} = \lambda_{max}\]

等号成立的条件为，当 $\lambda_{min}$ 或 $\lambda_{max}$ 对应的 $a_i = 1$，其余的 $a_i = 0$。

情况 1 其实只是情况 2 的特例。$a_i$ 充当挑选 $V$ 中列向量（即 $A^TA$ 的特征向量）的角色。

所以最小二乘解 $x^*$ 等于， $A^TA$ 的最小特征值对应的特征向量，也即 $A$ 最小奇异值对应的右奇异向量因此可以通过对 A 进行 SVD 分解求得 $Ax = 0$ 的最小二乘解。

而最小二乘的求解在多视角几何中均有应用，如路标的三角化、PnP等，因为这些问题最后会得到一个超定齐次方程。

参考

Total views. cowboys. Hits