Motor Selection
估算选型
- 无人机重量:1kg
- 螺距:3英寸(7.26cm)
- 直径:90mm
- 螺旋桨重量:2.35g
给定以上条件,给电机选型,从已有的两种电机二选一。
确定悬停所需转速
首先考虑推力和转速的关系,便于从无人机重量反推悬停所需转速。根据动能定理:
\[Q = A \cdot (v_{in} + \Delta v_{1})\] \[\begin{align} T &= m \Delta v \\ &= \rho Q \cdot \Delta v \\ &= \rho A \cdot (v_{in} + \Delta v_1) \cdot \Delta v \\ &= \rho A \cdot (v_{in} + \frac{1}{2}\Delta v) \cdot \Delta v \\ \end{align}\]其中:
- $Q$:单位时间通过的空气体积
- $T$: 推力[N]
- $\rho$:空气密度[kg/m^3],标准大气压下取 1.225kg/m^3
- $A = \frac{\pi D^2}{4}$:螺旋桨扫掠面积[m^2],$D$ 为螺旋桨直径
- $\Delta v = \frac{1}{60}nP$:流出空气增加的速度,或螺旋桨有效速度[m/s]
- $n$ 为转速[rpm],$P$ 为螺距[m]
$\Delta v_1 = 0.5 \Delta v$ 可由伯努里方程求解得到,这意味着螺旋桨盘处,空气速度增量是空气最终增加速度(诱导速度)的一半。计算过程参考 螺旋桨基础理论。
考虑无人机在无风环境中悬停,则 $v_in = 0$,代入得:
\[T = \frac{1}{2} \cdot \rho \cdot \frac{\pi D^2}{4} \cdot \left( \frac{1}{60} nP \right)^2\]如果使用上述桨叶,且无人机重量为 1kg,则悬停转速为
def cal_hover_rpm(T, rho, D, P):
n = np.sqrt( T / ( 0.5 * rho * 3.1415926 * (D**2) / 4 * (P/60)**2) )
print("n_hover[rpm]: {}".format(n))
In [43]: cal_hover_rpm(T, rho, D, P)
n_hover[rpm]: 20723.21720329751
In [48]: print(T, rho, D, P)
2.45 1.225 0.09 0.0726
另一种算法:
\[T = C_T \rho (\frac{n}{60})^2 D^4\] \[n = 60 \sqrt{\frac{T}{D^4 C_T \rho}}\]$C_T$ 是螺旋桨拉力系数,一般取 0.1 到 0.2。
In [44]: n = 60 * np.sqrt(T/(D**4 * 0.1 * 1.225))
In [45]: n
Out[45]: np.float64(33126.93299999689)
In [46]: n = 60 * np.sqrt(T/(D**4 * 0.2 * 1.225))
In [47]: n
Out[47]: np.float64(23424.278964210218)
可以看到 $C_T = 0.2$ 时,计算的结果和第一种方法比较一致。
计算悬停增益
接下来考虑电机的一阶动力学(first order motor dynamics),如下
\[U = \frac{JR}{K_e} \dot{\sigma} + \frac{C_Q R}{K_e} \sigma^2 + K_e\sigma\] \[K_e = \frac{30}{\pi K_v},\ K_v\ unit:[\mathrm{rpm/V}]\]如果忽略 propeller drag,即 $C_Q= 0$,且电机匀速转动,则
\[U = K_e \sigma = \frac{30\sigma}{\pi K_v} = \frac{60\sigma}{2\pi} \frac{1}{K_v} = \frac{n}{K_v}\] \[\begin{align} n = 20723 \mathrm{rpm},\ K_v = 1700 \mathrm{rpm/V} &\Rightarrow U = 12.19 \mathrm{V} \\ n = 20723 \mathrm{rpm},\ K_v = 3000 \mathrm{rpm/V} &\Rightarrow U = 6.91 \mathrm{V} \end{align}\]对电机的一阶动力学线性化,线性化点为电机悬停转速 $\sigma_h$,并进行拉普拉斯变换得到传递函数:
\[\frac{\Delta \sigma}{\Delta U} = \frac{\frac{K_e}{2RC_Q\sigma_h + K_e^2}}{\frac{J}{2C_Q\sigma_h+K_e^2/R} s + 1} = \frac{g_{dc}}{\tau s + 1}\]选择合适的 $R$ 和 $K_v$ 来最大化 $g_h$,可以观察到我们需要尽可能地让 $R$ 和 $K_v$ 尽可能地小。$g_h$ 越大意味着转速对电压变化的响应越敏感,机动性越强。
def cal_gain(sigma_h, Kv, J, R, CQ):
Ke = 30 / (np.pi*Kv)
gdc = Ke / (2*R*CQ*sigma_h + Ke**2)
tau = J / (2*CQ*sigma_h + Ke**2 / R)
gh = gdc / (tau * sigma_h + 1)
print("gdc: {}, tau: {}, gh: {}".format(gdc, tau, gh))
In [38]: cal_gain(2170, 1700, 1e-5, 221e-3, 0.0)
gdc: 178.02358370342162, tau: 0.07004019594368625, gh: 1.1636499941302458
In [39]: cal_gain(2170, 1700, 1e-4, 221e-3, 0.0)
gdc: 178.02358370342162, tau: 0.7004019594368625, gh: 0.11705360754125838
In [40]: cal_gain(2170, 3000, 1e-5, 90e-3, 0.0)
gdc: 314.1592653589793, tau: 0.08882643960980423, gh: 1.621438940385837
In [41]: cal_gain(2170, 3000, 1e-4, 90e-3, 0.0)
gdc: 314.1592653589793, tau: 0.8882643960980423, gh: 0.16290058033161212
小 kv,大扭矩,匝数多,内阻高(细缠绕,减少发热,$P_{loss} = \frac{U^2}{R}$),追求低速大扭矩,关节电机
大 kv,小扭矩,匝数少,内阻低(减小铜损,$P_{loss}=IR^2$),追求高转速
| kv[rpm/V] | R[mOhm] | tau[s] | 直流增益 |
|---|---|---|---|
| 1700 | 221 | 0.070 | 178.02 |
| 3000 | 90 | 0.089 | 314.16 |
结论
- 从响应增益的角度看,选择 kv3000 更合适
- 从响应延迟的角度看,选择 kv1750 更合适
- kv1700 的电机若用 4s 的电池,悬停油门 75% 左右,过大,不匹配,因此应使用 6s 电池驱动 kv1700 电机
实测
KV3000 电机飞行的结果如下图,使用 4s 电池,初始电压 16.2V,悬停阶段降至 13.3V,此时的电机油门大小为 0.6,有效电压为 7.98V,可计算出此时的转速:
\[n = K_v U_e = K_v \cdot Thr \cdot U_{in} = 3000 \times 0.6 \times 13.3 = 23940 \ \mathrm{rpm}\]实测转速和估算转速十分接近,验证了该估算方法的可行性。
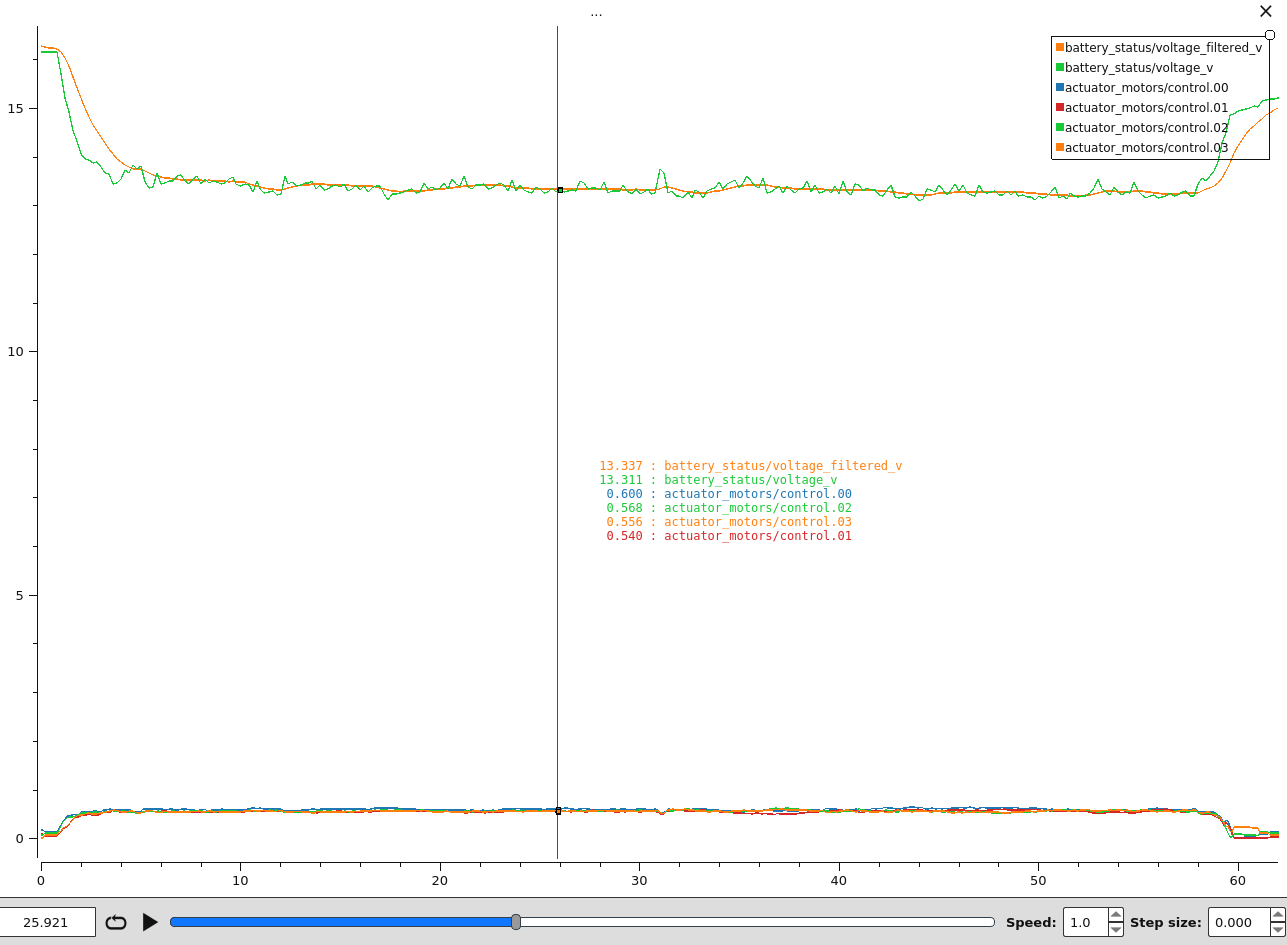
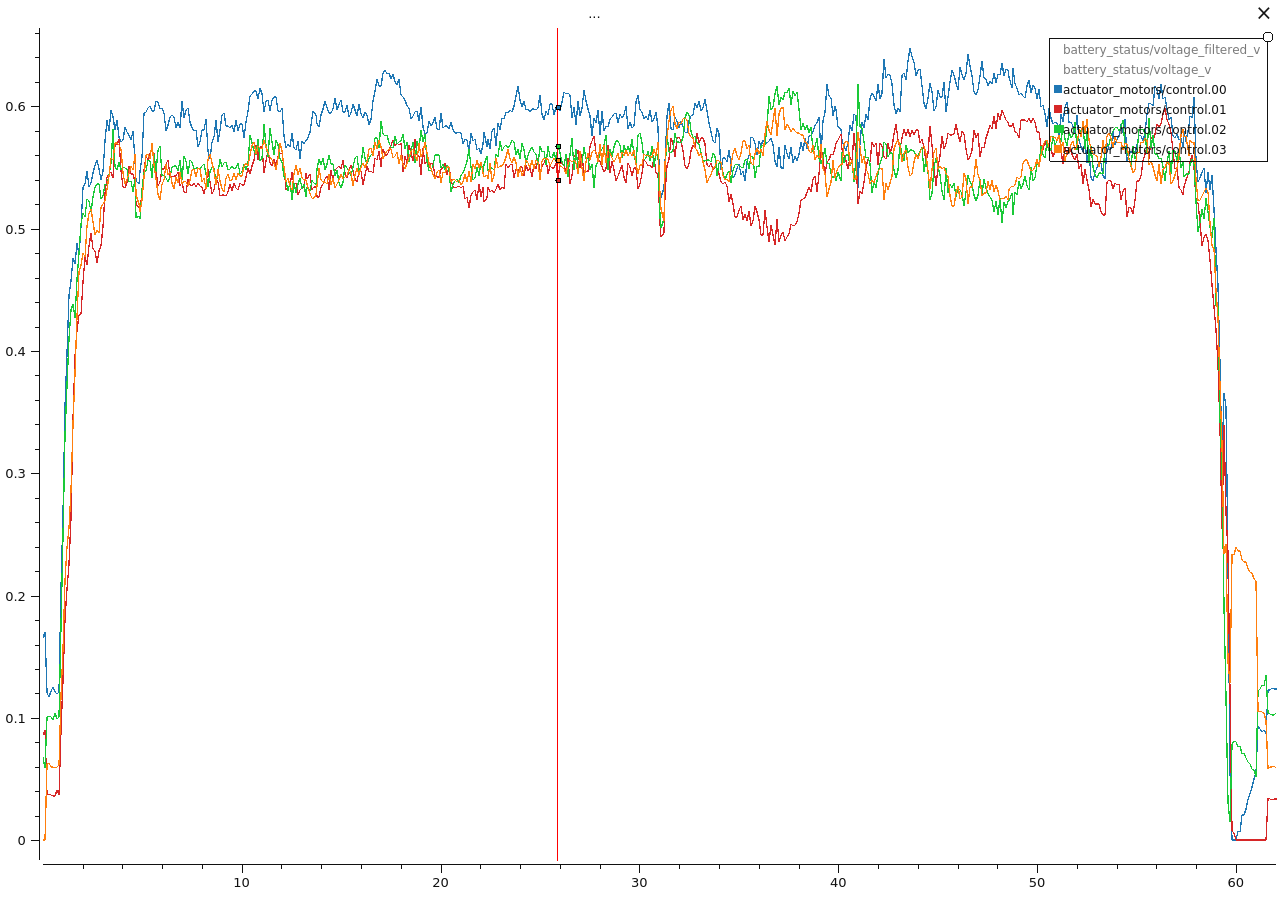
另外,四个电机的转速不平衡,一号电机的转速会大于其他三个电机,其现象是如果电机转速均保持一致,也就是摇杆的 yaw 不打一定偏移量,无人机会慢慢朝左转。
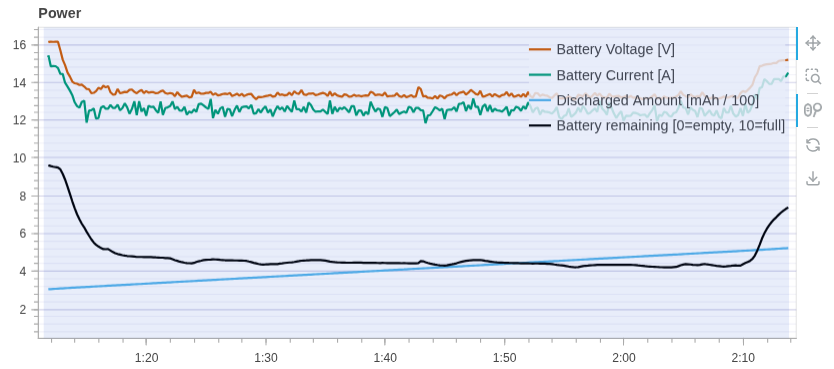
电流电压在悬停时均变小,如下图。
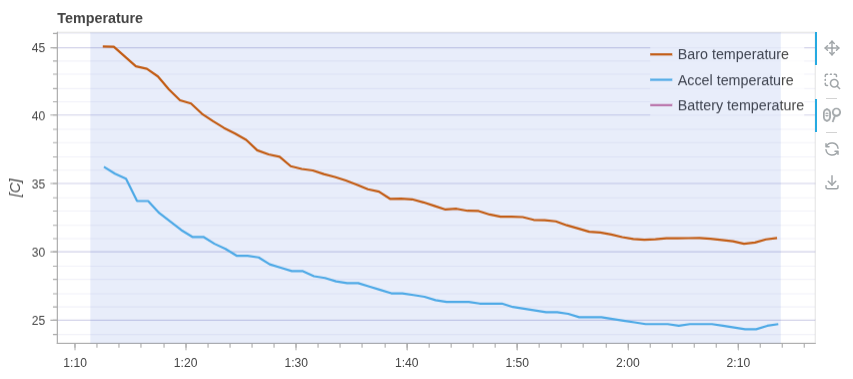
温度变化如下图,变化幅度约 10 度。
其他
一帧DSHOT600由16个比特位构成,其中前11位是油门信号,第12位是telemetry请求标志(tlm需要电调硬件支持),后四位是CRC校验位。速度600kbits/s,一帧信号的长度为26.7us。